John A. Medeiros
Look through any text on vision or any article from the current literature on color vision and you will invariably see a statement very much like the following: Color vision is provided by the existence of three separate classes of cones; a red, a green, and a blue sensitive type.
This explanation, an obvious way to account for the apparent three-dimensional nature of human color vision, is repeated so often and so unequivocally that it is no longer questioned in any serious way. Its experimental support must surely be so solid and unimpeachable that no one should even think of questioning it. So that’s it, end of story, right?
Well, perhaps not quite…
To make a bad pun of it, there is more to this than meets the eye. This classic model of color vision, first proposed in its essentially modern form by Thomas Young more than two hundred years ago, is presumed to work in a manner wherein each of three types of cones detects light with a probability determined by the absorption spectrum of the pigment it contains (Young, 1802). Thus, the cone containing the “red” absorbing pigment preferentially signals detection of the longer wavelengths of light. Of course, by itself, a signal from a ‘red’ cone does not actually say that red light was detected, only that a detection event occurred there and that the probability of that detection was proportional t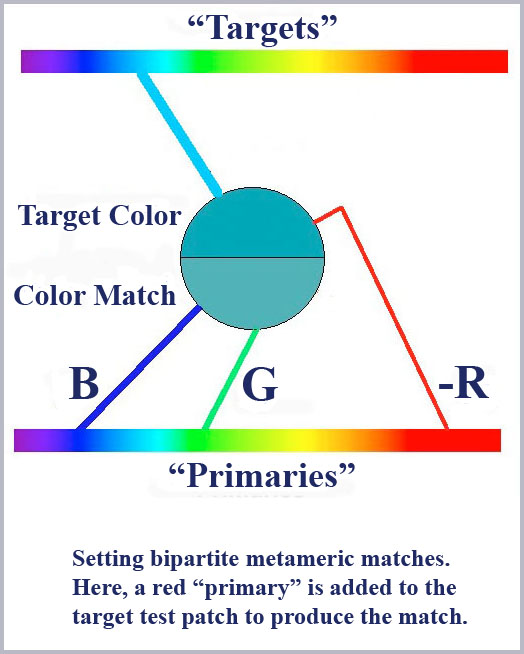
o the value of its pigment absorption spectrum, larger for a longer wavelength, red light.
Similarly, the other cone classes preferentially signal their detection of the other regions of the spectrum. The perception of color is then to be synthesized through the processing of the information from all the cone classes by inter-comparison of the relative responses of each cone type to a given source of light. So, for example, a set of outputs of about equal parts from the red and the green cone classes with little signal from the blue cones would be interpreted as an indication of the presence of yellow light.
In the classic test for evaluating the appearance of patches of color with different spectral composition (metameric color matches), an observer is set the task of equating the appearance of two separately illuminated halves of a small field. One half is the arbitrarily illuminated target portion to be matched and the other half of the field is a superposition of the variously tuned intensities of the ‘primaries’ one tweaks to get the match. In practice, it is necessary to add one of the primaries to the target half for this to work. This is equivalent to using a negative value of the primary (adding to the target half is like subtracting from the primaries half).
Early researchers tried valiantly, without much success, to search for the three unique primaries in these matches that would correspond to the presumed three fundamental cone primaries of the eye. However, virtually any three primaries can work so long as they satisfy a couple of basic conditions (roughly orthogonality and completeness): no combination of any two of them can be matched to the third and some combination of the relative intensities of the three primaries can produce white.
In any case, whether or not such unique primaries can be easily identified, the three dimensional nature of color matching still proves that there are three types of cones anyway. Right?
Well, not exactly…
Next Page: Three-Cone Model is Experimentally Falsifiable