John A. Medeiros
First of all, while color vision exhibits limited dimensionality, that in itself is not proof that the limitation comes about because there are distinct kinds of cones. It is a separate step to prove that one follows from the other. After all, you would have to rule out that the three dimensional nature of color vision is not caused by something else (and there is good evidence for just that, which we will elaborate on subsequently).
Most importantly, however, the premise that the three dimensional nature of color vision is imposed in the first step of the visual process by partitioning detection events among three kinds of cones is directly contradicted by experimental observation.
It was, in fact, shown to be false by Herbert E. Ives some ninety years ago (Ives, 1918). Despite the straightforward and unequivocal nature of his test, this experimental result has been all but forgotten and its message has been totally ignored by the experts in the field.
Consider, again, the basic premise of the three-cone model and how it works. The view is that each cone simply reports how much light it detects, its so-called ‘quantum catch’. This (presumed) univariant response of the cone itself has no intrinsic information about the color of the light it caught. In this view, that spectral information is discarded in the very first step of visual perception and is not retrievable by any subsequent manipulation of the cone output signals. It is only by comparing the relative output of each of the three cone classes that the color of the incident light is synthesized.
Look at a simple case of how this operates, in the perception of yellow, for example. We know that there is more than one way to make a yellow light. One could simply use a monochromatic yellow sliced from the visible spectrum at a wavelength of about 580 nm. One could also use a mixture of red and green light. By adjusting the ratio of red and green (essentially an equal amount of each for color normal observers), one can make a compound yellow that essentially matches the pure monochromatic yellow. This is simply a direct consequence of the limited dimensionality of color vision. These two yellows (a pure monochromatic yellow and an appropriate mixture of red and green) are simply a metameric match. In the three-cone model, any information that they were created in different ways is lost and is irretrievable. That information was discarded in the very first stage of the visual process and the two yellows look the same because they excite the ‘red’ and ‘green’ cones identically.
However, Ives’ experiment shows that this is not true and the three-cone model is wrong. He did this by first superimposing a red and green bar of light so that it looked yellow. He then scanned this compound yellow light across the field of view of the observer. What he found was that as the compound yellow moved across the retina, color separation occurred so that the bar had a leading red edge, a yellow middle, and a green trailing edge.
Well, ok, one might say, that simply means that the ‘red’ cones must have a faster response time than the ‘green’ cones and turn on first as the bar moves across the retina and stimulates the receptors while the slower ‘green’ cones turn off later than the ‘red’ cones as the bar passes by, leaving the yellow sensation in the middle. So far so good, although there is no obvious explanation about why ‘red’ cones and ‘green’ cones, which for all intents and purposes are otherwise identical except for the slight difference in the photopigments they contain, should have a different response time in any case. But, for the sake of argument, say that they do and the separation of the compound yellow is thus explained.
Now what happens if you try this with a pure, monochromatic yellow? In the standard three-cone model we have been discussing, the same thing must happen. Since it appears yellow because of the equal excitation of the red and green cones the way a mixed yellow does, it cannot be differe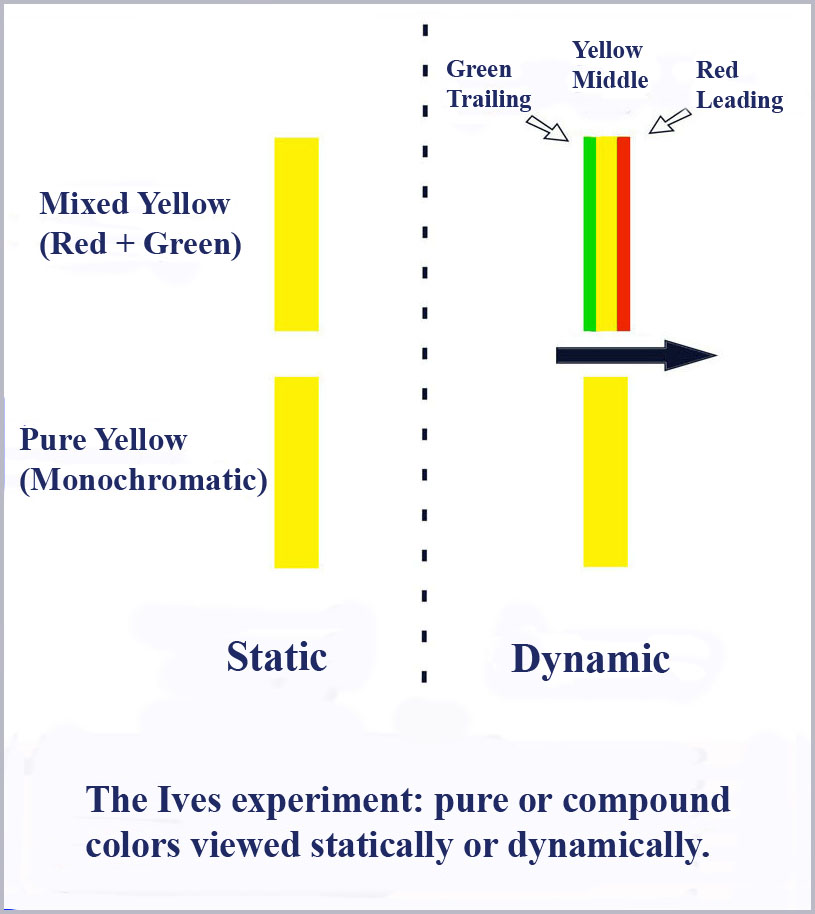
nt. Right?
Wrong!
When a bar of pure yellow is moved across the retina, it does not separate into a red leading edge and a green trailing edge. Rather it retains the same yellow color throughout. In Ives’ own words:
"The next point taken up was the behavior of the pure yellow, adjusted to be a subjective match with the compound yellow, and arranged to exactly take its place between the red and green. It was at once apparent that pure yellow does not separate into red and green. This fact is strikingly shown by arranging the slit so as to be all compound yellow, except a small portion of pure yellow. When stationary the slit appears alike throughout its whole length in brightness, hue and definition. But upon moving the image sideways, or oscillating it, the compound yellow immediately broadens out and becomes ill-defined, the pure yellow remaining narrow and sharp" (original emphasis).
So this flat out says the standard three-cone model must be wrong. End of story? Well surely not you might say. After all this is only one experiment and it was done almost a hundred years ago. None of the experts have paid any attention to this result, so, did Ives get it wrong? Is it repeatable?
I wondered that too. This result is so important and so unequivocal that it should be repeated and verified (or invalidated). Many times. My colleagues and I have repeated the experiment and we did indeed get the same result (and a good bit more actually).
Several years ago, I assembled an apparatus consisting of multiple monochromators to provide bars of light of tunable color that could be optically combined through beam splitters and adjustable in position so that the bars could be separated or superimposed. This output was then directed into the eye after reflection from a scanning mirror. A critical condition that has to be provided for this to work is a fixation light. That is, it is necessary for an observer to be looking in one fixed direction so that the moving bar(s) of light will scan across the retina of the eye. It is also important to do this in a darkened room to make the phenomenon easier to see.
If one superimposes a red and a green light tuned to look uniformly yellow when stationary, then as the bar is moved and one looks straight ahead as the bar scans across the retina, you will indeed see – as we did- the compound yellow light to broaden out with a leading red fringe and a trailing green fringe. If you tune both outputs to be monochromatic yellow and repeat the scanning, you will find - again as we did – that it has no such color separation, verifying the Ives’ result and falsifying the three-cone model of color vision.
When my colleagues and I did this experiment, we did find a good bit more than just the verification of Ives’ result (Medeiros, Caudle, and Schildt 1982). Under carefully controlled conditions, we also observed a whitish, shimmering afterimage trailing behind the colored bar by an amount that depended on the speed of movement of the bar (and its color and intensity). Now afterimages are not a new thing and are, after all a common part of everyday experience. Indeed, an afterimage similar to the one we are talking about here has been known and studied for over a century. That afterimage effect goes by various names, including Bidwell’s Ghost, Hamaker’s Satellite, and the Pursuant Image. However, what we are discussing here is not this afterimage effect (with a time delay on the order of a few hundred milliseconds) but something entirely different with an order of magnitude shorter time constant, on the order of a few tens of milliseconds.
While the details can be found elsewhere (in the book, Cone Shape and Color Vision: Unification of Structure and Perception- Medeiros, 2006) we mention here that we conducted a series of experiments to demonstrate that this whitish shimmer was, in fact, the direct perception by the rods and not an afterimage as such.
We were thus able to separately and simultaneously observe the direct and separate perception by the cones (the colored bar) and the rods (the following shimmer). 
Since we were able to experimentally demonstrate that the delay of the rod perception itself was totally independent of the wavelength of the inducing light, we could use it as a reference to time how much shorter the latency of perception was for each color by the cones. What we found was a monotonically increasing delay in the perception of color as wavelength is decreased. This, in fact, is what accounts for the separation of red and green perception.
Now, the effort to measure the chromatic latency of human color perception has enjoyed a long, tortured and controversial history. For example, Uttal (1973) tabulates a list of eighteen separate reports on attempts to measure chromatic latency by a number of different techniques. In that list, eight studies reported no variation in chromatic latency as a function of wavelength, four reported a longer time constant for longer wavelengths, and six reported a shorter time constant for longer wavelengths. This muddled result is a reflection of the difficulty in measuring the small time differences involved (only a few tens of milliseconds) by various reaction time techniques or of separating the effects of phase differences and true time constant differences in the various approaches employing flicker minimization by alternating colors. Moreover, given that the intensity of a given color can also affect is apparent delay time, it can be difficult to separate intensity effects from purely chromatic effects in these measurements.
In our studies using the wavelength-independent rod response as a reference, we were able to conduct latency measurements of each color with a resolution on the order of two milliseconds (Medeiros, 2006). We also conducted the latency measurements at near threshold intensities for each color to minimize the intensity dependence of the effect. Our measurements were repeated numerous times, on a number of different days for two color normal male observers.
We did not find three separate groups of delay times, but rather that the latency was a direct linear function of decreasing wavelength. While it was not possible to measure the absolute time delay of the color perception, we were able to relate the time delay of a given color perception relative to that of another color percept (we actually measured the time the chromatic perception led the achromatic rod perception). Our experimental results for the time delay (in milliseconds) can be expressed for any wavelength, λ (in nanometers) relative to the perceptual delay of a 650 nm red light to be approximately: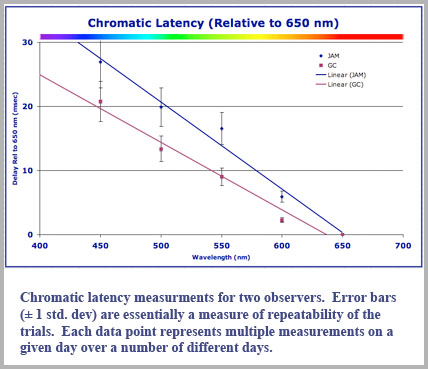 
Delay (msec) = 97.5 - 0.15 λ (nm).
This gives a delay of 0 msec for red light of 650 nm (relative to itself) as it should and a delay of 30 msec for the shortest wavelength of light we tested, 450 nm in the blue.
Our data for two color-normal male observers is shown in the accompanying plot. While the two observers had latency values that were slightly different, both exhibited essentially monotonically increasing delay for shorter wavelength.
So all this begs the question, just how does human color vision work? What might this time delay have to do with it and how could it even come about? But wait, surely we can’t be done with the three-cone model, after all there is direct evidence that different photopigments are present and this must mean that the three cone classes have been proven to exist, right?
Well, again, not exactly…