Color Vision: A New Understanding

John A. Medeiros

 

The Cone Spectrometer Model (CSM)

Just as in an investigation of a crime scene where one tries to determine who has the means, the motive, and the opportunity to commit a crime, we could apply this approach to the investigation a new model of color vision and see if it is a plausible or provable candidate.  Starting with opportunity – can the model work, is it physically possible?  Turning next to means, how could it be implemented in a workable model of the process in terms of the physical, chemical, and biological components present in the eye?  Finally, examine the motive, what is such a model good for and does it explain the facts of color vision better than some other theory? 

While fitting this examination of a proposed color vision model within the context of crime scene investigation is a bit of a stretch, it can still be rather useful approach to putting the pieces together to try to better understand human color vision.

First the opportunity; what is the model and is it physically possible? 

The Opportunity

To begin with, we should take note of the fact that the understanding that the photoreceptors are optical waveguides is well established.  The receptors have a higher index of refraction than the medium in which they are immersed so that the conditions for light guiding within the rods and cones exist.  The particular values of the refractive indices of the receptors and their surrounding medium, the exact dimensions of the receptors, and the launch conditions for light entering the receptors will all influence just what waveguide modes are propagating within them. 

Low-order waveguide modes propagating in the receptors have been directly observed in microscopic examination of excised retina (Enoch, 1960, 1961, 1963).   It is widely accepted that the explanation for the Stiles-Crawford Effect of the First Kind (SC-I) whereby light incident off-axis on the receptors excites them less efficiently than on-axis light, is a consequence of waveguide behavior (Snyder & Pask, 1973). However, despite the evident existence of waveguide mode propagation within the retinal receptors, there has been widespread resistance among vision scientists to the consideration of any possible role for waveguide effects in basic receptor function.

Part of this resistance is because of the mathematical complexity of computing the details of waveguide mode propagation.  However, the physical explanation of what happens in a small, tapered fiber (a cone) is relatively straightforward.

First, what are these waveguide modes?  Essentially, each waveguide mode is light propagating within a fiber at a specific angle to the fiber axis.  When the fiber is large (as scaled by the wavelength of the light being propagated) many modes (propagation angles) are allowed and the fiber acts as a simple conduit piping light along its length through total internal reflection at the fiber-surround interface.   

However, as the fiber decreases in size, the number of modes or propagation angles that “fit” within the fiber decreases due to the wave nature of light itself (essentially wave interference effects).  As conditions become more restrictive, the various modes are said to be cutoff.  Computed mode cutoff curves are shown below for the two lowest-order modes (the so-called HE21 and HE11 modes).  These curves plot the efficiency of an optical fiber, defined as the ratio of light propagated within the fiber to that propagating outside the fiber in its so-called evanescent wave, as a function of waveguide “size”.  As the efficiency drops to zero, light is no longer confined to the fiber and it then radiates away.  The measure of 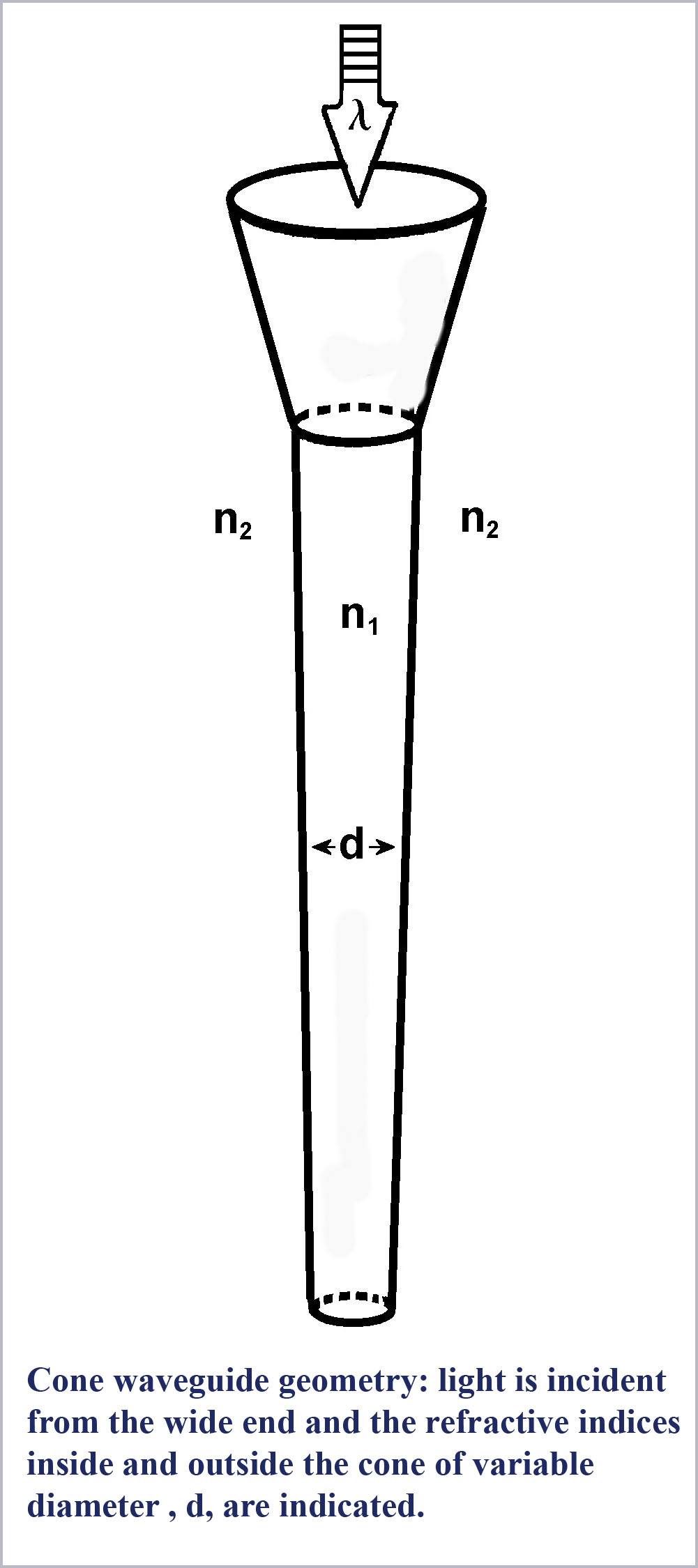waveguide “size” against which this efficiency is plotted is the dimensionless waveguide parameter, V.  This parameter is defined to be

                                    V= (πd/λ)(n12– n22)1/2

where d is the diameter of the waveguide, λ is the wavelength of light (in the same units as d) and n1 and n2 are the refractive indices of the material inside and outside the guide, respectively (π is just the usual constant circumference to diameter ratio of the circle). 

So this measure of waveguide “size” becomes smaller as either the physical diameter of the guide becomes smaller or the wavelength of the light is larger.  The waveguide size also decreases for smaller differences in refractive index between inside and outside the guide. Referring then to the cutoff curve of the HE21 mode in the figure, we see that the mode is abruptly cutoff (its efficiency drops to zero) for a value of the waveguide parameter of about two and a half (actually at V = 2.405…, a value related to the zeros of a Bessel function which is mathematically used to describe the waveguide propagation conditions).  This relatively abrupt cut off of the HE21 mode is typical of all the higher-order modes of the waveguide (not shown in the figure).

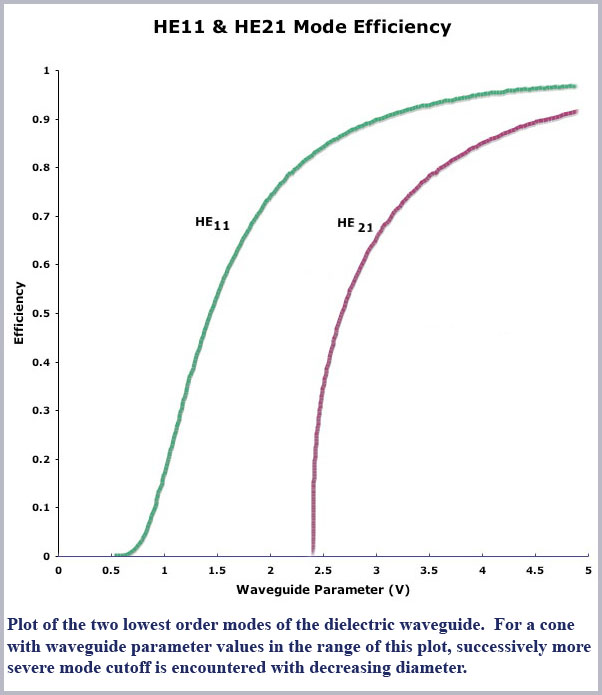
Now, at even smaller values of V, below this value of 2.405, only one mode can propagate, the lowest order, so-called fundamental or HE11 mode.  This mode too drops in efficiency for even smaller values of V although not quite so abruptly as all the other, higher order modes. Note, though, that the efficiency of this mode is essentially zero by a value of V of about 0.6 so that below this value virtually no light is propagated within the fiber (it is all outside of the fiber in its evanescent surface wave).

So what would all this mean in terms of discriminating color?  Consider that cutoff, the shunting of light from the inside to the outside of the fiber, becomes more pronounced as the fiber diameter decreases.  So, for the right conditions, as light enters a cone from its broad (base or proximal) end and propagates down the cone towards its narrower (tip or distal) end, as it does in the retinal cones, light will be progressively shunted out of the interior of the cone.  This effect will be differential with wavelength since the cone is effectively “smaller” for larger wavelengths.  Thus, for a full spectrum of white light entering the base end of a properly sized cone, long wavelength red light will be shunted out first, with progressively shorter wavelengths being shunted out as the cone diameter decreases along the propagation direction.  That is, the cone shape itself will produce a spectral dispersion of the incoming light along the length of the cone.  Such a cone is essentially a miniature spectrometer. Detect the length-dependent distribution of light along the cone and you can discriminate colors.

Now there are separate questions about whether it is possible to detect this spectral information in a way that is consistent with the physics and physiology of the retina and if the quantity and quality of the color information you could get this way is consistent with what is known about color vision.  We will show that the short answers to these questions are "yes" and "yes", however we would be getting ahead of ourselves since we are still discussing the “opportunity” of this model, is it a possible one?  

Here, I have simply made a physical argument about how this spectroscopic effect would work.  More details about the mathematical description and the theoretical underpinnings of this effect can be found in the book, Cone Shape and Color Vision: Unification of Structure and Perception.  We would like to confine ourselves here to the big picture and how it fits in within the lines of evidence.  So, given this general description of the process, is it a physically realizable one and if it is, could it be present in the cones of the human retina?

While the prediction of the effect follows directly from the basic physical and mathematical description of waveguide propagation (although, astonishingly, this spectroscopic effect has not been mentioned, discussed or predicted anywhere else that I am aware of) what about a physical demonstration of the effect?  If you send light down a fiber of decreasing diameter can this effect be seen? 

To explore this effect, I heated a quartz rod near its middle with an acetylene torch and allowed gravity to pull down on the lower half to produce gently tapering ends on two rod halves as it was stretched apart.  I then immersed one of these tapered fibers halves in a liquid with the refractive index adjusted to be only very slightly less than that of the tapered rod.  Then, illuminating the rod top (entrance end) with a focused beam of white light, I took microphotographs of the light leaking out of the rod near the very small tapered tip.

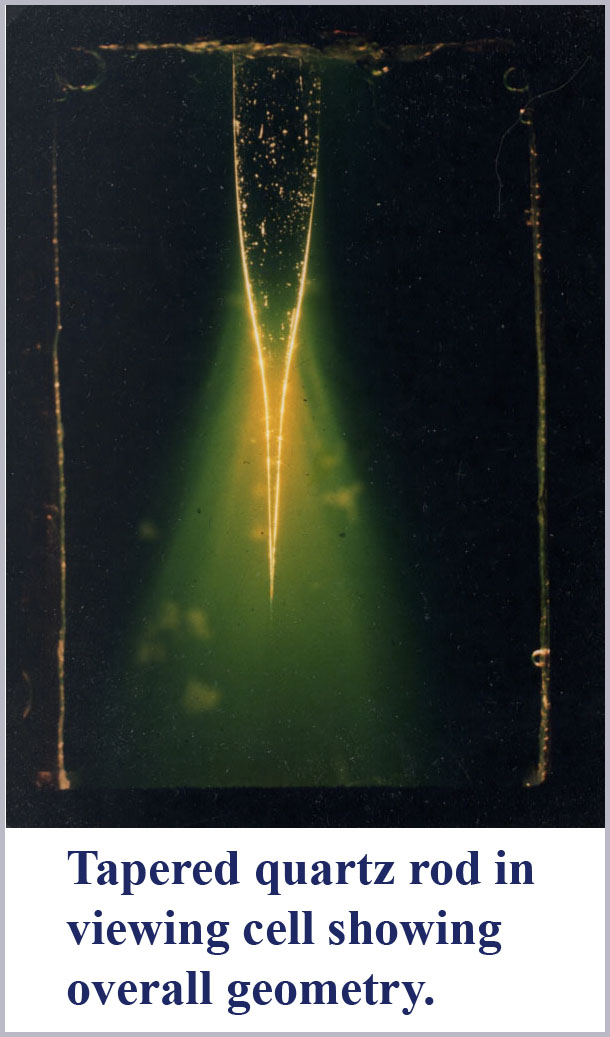
The figures show the result.  As predicted, light is spectrally dispersed by mode cutoff at the tapered end of the fiber.  Two photographs are shown. The first is an overall perspective view showing the setup with a tapered rod in the cell containing the index matching liquid. White light is focused into the top of this rod and large light losses are evident through the tapered portion of the rod. The yellow-greenish cast of these light losses are due to the fluorescence of the disodium fluorescein dye dissolved in the medium surrounding the rod which was used to help visualize the radiative losses from the tapered rod. Near the very tip of this tapered rod, one can barely make out some color differentiation along the rod wall.

The second photograph is a highly magnified view taken with close-up optics of the very end tip of this tapered rod. Evident here is the spectral dispersion due to mode cutoff along the outside of the fiber with the longer wavelengths being excluded first. The shortest wavelength light is the last to be seen along the wall of the tapered fiber until there is nothing left within the cone structure. If one looks carefully, it is also evident that there are two mode cutoffs occurring. In the taper near the top in this micrograph, the evanescent wave is first reddish, then passing through to a pale blue before the last mode cutoff occurs showing the entire progression of spectral colors. Notice that the first mode sequence to cutoff here (presumably due to HE21) occurs over a shorter distance than the final sequence due to HE11cutoff. This is in accord with the expected more abrupt cutoff of the second-order mode as compared to the lowest-order fundamental mode.

So, the effect is possible in principle and is physically realizable.  Is it present in the human cones?  Absent direct observation (which would be exceedingly difficult to do for the very fragile and delicate living retinal tissue where high magnification is required) one needs to know the actual values of the cone diameters (relatively easy) and the values of the refractive indices inside and outside the cones (very difficult).

The dimensions of the cone outer segments can only be determined on dead tissue where one has to fix and preserve the delicate retinal material with necessarily somewhat uncertain consequences on its exact form and dimensions.  This has been done by many observers under various protocols for both human retinal samples as well as that of various, closely related primate species.  There is some variability from observer to observer on the cone dimensions reported although there is a general concurrence that the photosensitive outer segment portion of the central (foveal) cones of the retina has a maximum diameter of about 1 µm (about two times the diameter of the wavelength of visible light). Significantly, there is, as well, a pronounced systematic progression of retinal cone shape from the central (foveal) region to the peripheral portion of the retina. 

The best “big picture” of these dimensions is probably provided by the drawings of von Greef reproduced above and again here with the spectral dispersion of light excluded from the cones outer segments indicated. A schematic based on those and similar measurements is also shown below indicating the appropriate location in the retina of the progression of cone shape (note that the rods have the same shape throughout the retina). There is an evident systematic change in the cones from being long and gently tapering in the fovea to being shorter and more abruptly tapering in the periphery.  In this schematic, I have colored the cones with a representation of the light remaining in the cone along its length for white light initially incident.  Since longer wavelengths are excluded from the cone outer segments first, the light remaining in the cones is progressively bluer towards its distal tip until only the shortest wavelengths remain at the furthest end.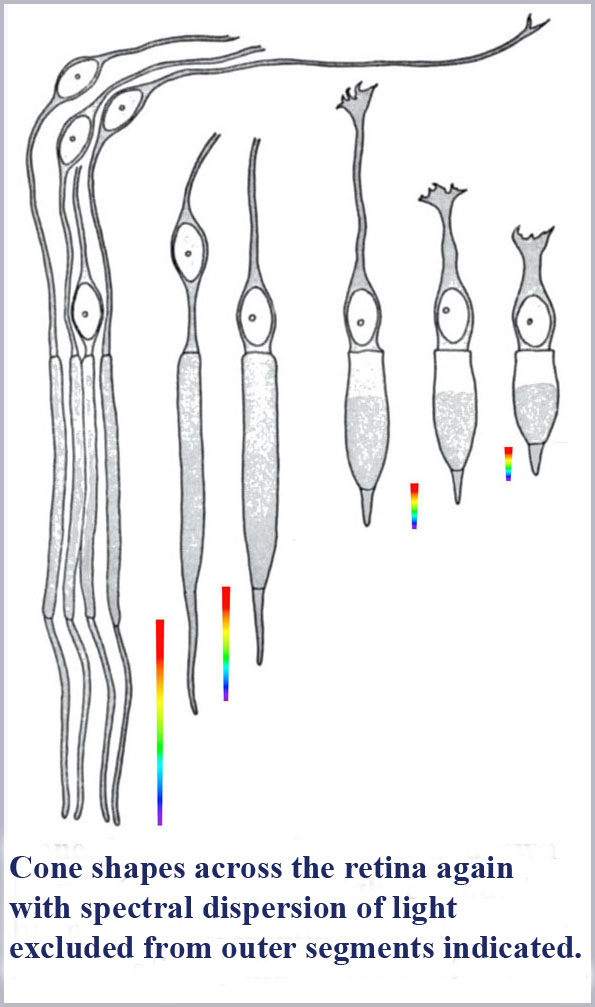

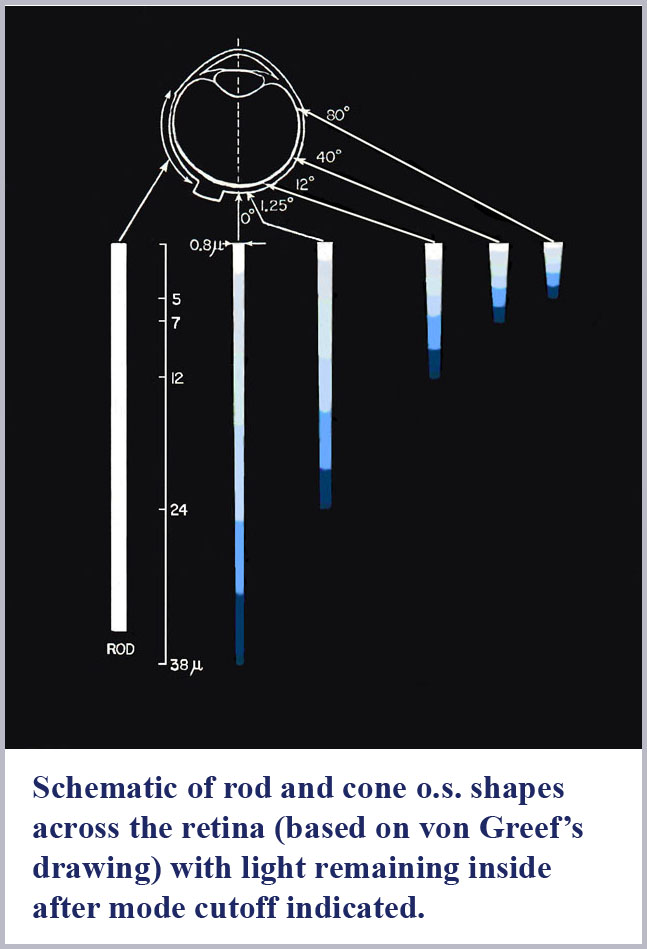
Not so incidentally, the foveal cones, because of their very slight tapering, have often been called rod-like in the literature.  Because they also provide the highest resolution color vision, this has led to the tendency by researchers in the field to discount the cone shape in any aspect of its functioning.  However, these foveal cones are tapered and the spread of the taper over their long length results in the spread of color dispersion over a greater length.  This has the result that these foveal cones will have the potential to be read with the greatest accuracy (for the same resolution of any read-out mechanism). 

To explicitly evaluate the tapering of the foveal cones, my colleagues and I conducted anatomical measurements on (monkey) foveal cones where the retina was sectioned transverse to the axis of the photoreceptors (Borwein, Borwein, Medeiros, and McGowan, 1980).  Diameters of successive slices along the cone outer segment length were measured at their smallest dimension (non-perpendicular slices would give an elliptical shape with the ellipse minor axis being the cone’s true diameter at the sectioned position).  While this anatomical study (and others, of course) revealed a wealth of structural detail present in the photoreceptors, the net result of these measurements is that foveal cones are somewhat less than 1.0 µm (1000 nm) in diameter at the beginning of the photosensitive outer segment and taper to about 0.6 µm near their tip.  Over the roughly 40 µm lengths of the outer segments, this gives a full cone taper angle of just over half a degree.  This indeed is barely different in appearance from a true rod, but the 40% diameter change over the length of the cone can produce substantial dispersion of the spectrum if the refractive indices are properly tuned (note that the difference in wavelength between 650 nm red light and 450 nm blue light is just over 30%).

There are very few measurements of receptor refractive index.  Perhaps the best are still that of Sidman (1957) who used a fluid index matching technique to get a value of 1.387 for the cone outer segments.  The refractive index of the medium surrounding the living receptors has not been directly measured although it has been estimated by Barer (1957).  The index of this medium cannot be less than that of saline (1.334) and must be somewhat larger because of the inclusion of suspended solids in the medium.  Barer suggested a value close to that of serum, 1.347.

So, using these values of refractive index for the cones gives their dimensionless waveguide parameter, V, to be:

V= (πd/λ)(n12– n22)1/2 = 3.14 (d/λ)(1.3872 -1.3472)1/2 = 1.04 (d/λ),

or to a good approximation, just the cone diameter divided by the wavelength of light (d//λ).  Thus the range (maximum to minimum) of V values in the foveal cones for the spectral range (450-650 nm) will span that of the largest diameter divided by the shortest wavelength (~ 1000 nm/450 nm = 2.22) to that of the smallest diameter divided by the longest wavelength (~ 600 nm/ 650 nm = 0.92).  Notice that this places the operating range of the foveal cones right in the middle of the cutoff region of the HE11 efficiency curve (2.4 to 0.6), ideal for spreading the spectrum along the length of the cone.

 So it all fits and the opportunity is there.  Now what about the means?  How could this Cone Spectrometer Model be implemented in a workable way to provide the color information in terms of the physical, chemical, and biological components present in the eye?  For that we turn to the means.

 

The Means

So far, we have seen that this cone spectrometer effect is theoretically possible, it can be physically demonstrated in appropriately dimensioned tapered fibers, low-order waveguide modes have been directly observed in retinal tissue, and the retinal cones are ideally dimensioned to exhibit the effect.  So the spectral dispersion described here is surely present in the retinal cones. 

Continuing to push the crime scene evidence analogy, the trick is now to determine the means or method by which the length encoded color information is deciphered.  Absent any direct connection to (say) three different portions of the cone along its length (for which there is no evidence) a good alternative is to convert the length code into a time dispersion encoding.  We already know that there is temporal dispersion in color information, with, for example, blue (450 nm) light perception delayed by about 30 msec from that of red (650 nm) light.  This value came from our measurements on moving bars of colored lights discussed previously, so converting to a time-correlated color code seems like a promising approach.

Now, light itself propagates at the enormous speed of 300,000 km/sec so we are not, of course, suggesting that there are any significant delays or associated conversion to a time code due to optical propagation.  However, conduction of electrical signals along nerve fibers are much slower than light speed, typically meters per second.  Moreover, the complex ion channel and membrane structure of the cone outer segments are more properly modeled as RC-circuits with (potentially) significant delay times.  Thus, time delays of millisecond duration in signals from the distal end of the cone compared to the near end would seem realistic.

Two critical items are needed for the length signal to be sensibly converted into a time signal.  First the source of the electrical transduction signal of light detection along the cone length must be uniquely associated with a location along the cone.  That is, each detection event must be localizable and the cone not act simply as a diffuse bag of photo-absorbing pigment with no ability to differentiate where along the cone length a detection event occurs.  Secondly, we need a synchronization signal to determine what signals are delayed relative to what.  The evidence is that the conditions necessary to satisfy both of these requirements are indeed present. 

First, consider signal localization. The diffusion of an electrical signal following a photoabsorption event in the cone has been both theoretically calculated and directly measured (Holcman and Korenbrot, 2004) to be localized to within 1 µm or less of the location of absorption.   Thus, a given single foveal cone could have its spectral dispersion over its length potentially readable to within one part in 40 (for a 40 µm long cone).  Note that the color discrimination potential for such a single cone is thus 1/40th of the spectrum dispersed over its length.  For a span of colors of 200 nm (650 to 450 nm) this can provide the potential to discriminate lights differing in wavelength by as little as 5 nm.  With more cones participating, we can expect the available hue discrimination resolution to be even better.

For the second requirement of a synchronization signal to read out the time code, we find that there exists a ready-made on-going syn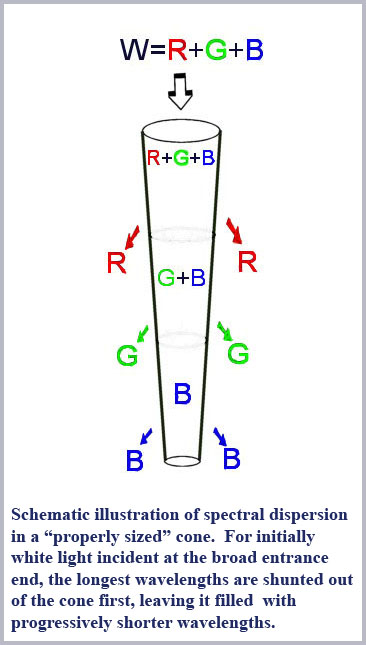c signal each time the eye undergoes a microsaccadic movement.  The existence of these microsaccadic eye movements has been known for a long time.  At first glance, it would be natural to assume that these motions are simply the result of residual instabilities in the control movements of the eye muscles directing the pointing of the eyeball.  So one would naturally have assumed that if these residual jerky motions could be removed by somehow stabilizing the image on the retina, that vision would improve. 

Now image stabilization has in fact been done by various experimenters through a number of different techniques with varying degrees of success in the complete stabilization of the retinal image.  What all these researchers have found is that vision, in fact, does not improve under these conditions.  Instead it gets much worse and within a very short time of the imposition of (complete) image stabilization visual function disappears altogether (Ditchburn & Ginsborg, 1953; Riggs, et al, 1953).

Now these microsaccadic movements are involuntary (occurring all the time), they are small (corresponding, on average, to the displacement of the retinal image by something like ten to twenty cone diameters) and frequent (occurring on average roughly ten times per second or so).  These motions thus provide a perfect synchronization signal for reading the cone’s color information.  Each time the light illuminating a cone changes (as a color border in the retinal image passes over it due to a microsaccade, for example) then a new read-out of the time delays of the signal coming from the length of the cone is possible. Note that this synchronization happens globally for all receptors over the entire retina. If there is no change in the illumination of the cone as a result of the saccade, there will be no change in the cone output. However, all cones that experience a change in their input as a result of the passage of a color border over the cone entrance (for example) will synchronously begin putting out a changed signal; the details of that change will depend on the color differences in the input illumination altered by the saccadic eye movement.

What would this signal look like and what information would it contain?  Changes in the early part of the cone output signal will result from differences in illumination in the part of the cone nearest to its output connecting synapse with the bipolars, its broad entrance end of the cone outer segment.  Here a signal can be generated by light of any color (including red, of course) since all light entering the cone passes through this part of the cone and can thus cause a photo-absorption (in proportion to the absorption spectrum of the photopigment there).  Signals coming slightly later, from the middle portion of the cone can be generated by changes in any color except red, since it has been shunted out of the cone by this point.  Signals coming latest, from the distal, small end of the cone uniquely signal changes in blue light since all the longer wavelengths have been shunted out by that part of the cone. Note that there is a degree of asymmetry in how signal changes are correlated with optical wavelength. Changes to the latter part of the cone signal can only be a result of changes in the short wavelength content of the illumination while changes in the early part of the cone signal can be caused by changes in the amount of any wavelength. This ambiguity is, however, removed on examining the entire signal change from the cone; if there is a change in the early part of the cone signal without a change in latter parts of the signal, then the change can be confidently assigned to differences in long wavelength illumination only.

Now this time code sounds like a convenient method for reading the color information, but is there any evidence that the eye actually uses a time-color code like this?  Actually, there is indeed direct evidence that the eye does use such a time-color code.  The existence of so-called subjective colors induced by appropriately modulated black and white illumination directly points to such a code.   Some 170 years ago Gustav Fechner (1838) noted that a complex series of colors could be induced with intermittent illumination. Perhaps the best-known example of this color induction effect is Benham’s Top, a half-black and half-white disk with circumferential black arc segments arraigned on the white semi-segment.  (These subjective color effects are also referred to as Fechner-Benham colors and also as Pattern-Induced Flicker Colors, PIFCs.)

A typical configuration of Benham’s Top is shown in the figure.  When the disk is spun at speeds around 8 to 12 times per second, one sees the arcs blur out to be continuous circles and to take on more or less desaturated colors.  For a disk configured as shown in the figure, upon counter-clockwise rotation, the outermost arcs take on a reddish color (often very bright red), the middle arcs a vague greenish-grey color, and the innermost arcs a dark blue or blue-black color.  If the direction of rotation is then reversed, the colors of the arcs are also reversed with the outermost being blue, the middle remaining green, and the innermost being red.

This subjective color phenomenon makes little sense in the standard model of color vision (and has not hitherto been plausibly explained by any model of color vision). Benham's Top was an invention of British toy maker CE Benham (Benham, 1894) and was a popular toy in Victorian times. The phenomenon has been extensively investigated for more than a hundred years and it has long been clear that it has something to do with the differential latency of different colors but there has hitherto been no coherent way to put these observations together in terms of  any model of how the eye sees color (Roelofs & Zeeman, 1958; Campenhausen & Schramme, 1995). The point here, of course, is that the time code of the Benham's Top is a direct consequence of how the proposed CSM model reads color information from the cones.

Since all observers see the same color ordering and the effect appears to be universally present (except that the effect has been inadequately explored for color blind observers, although at least one report states that colors are observed the same way, but less saturated - Stewart, 1924) then only a color vision model tied to the ordered timing of color perception would seem to make sense, i.e., a dynamic, rather than static, model of color vision. 

Note that on rotation, the back edge of the black half of the disk provides a time reference for the arcs on the white half.  The arcs that appear first (regardless of rotation direction) appear to be red and the arcs appearing last appear to be blue.  There are a number of good examples of Benham's Top on the Web where one can vary the dynamic parameters to see the induced subjective colors. Two good ones include a java script version where one can use the computer mouse to change the disc rotation here and a version where one can vary the parameters with mouse clicks here. I should point out, by the way, that the induced colors are not actually produced on the black part of the arcs themselves. Rather, they are induced at the border between the black arcs and the white surround. For arcs of sufficiently small width, the color "bleeds" over so that the entire arc does look colored. If the arcs are made too thick, the colors will be less evident.

So, what about the time scale for the phenomenon – does it make sense in terms of the time delays we have been talking about for the retinal cones?  For a typical rotation rate of 10 Hz and the arc distance of 120o between the start of the red and blue sensations on the rotating arcs, the time delay is 1/3 of 1/10 of a second or 33 milliseconds.  This time difference is in very good agreement with the measured time delay between the perception of red (650 nm) and blue (450 nm) light we discussed before, namely 30 milliseconds.

So the means are there – the cone spectrometer model could indeed work by conversion of the length dispersed color information into a time code. Photoabsorption events along the cone length can be localized to one micrometer or less and the microsaccadic eye movements provide a natural, global synchronization signal to coherently encode the color information.

What then about the motivation?  Why would we want such a model, what is it good for and does it explain the facts of color vision better than any other theory?

The Motive

So the question is: is the motivation there and does the Cone Spectrometer Model (CSM) as described here have any utility?  Does it explain color vision in a sensible way and can it explain the myriad aspects and phenomenology of human color vision? 

Again, we would suggest that the short answer is "yes"; it does address and directly explain many aspects of how human color vision seems to work.  To this point we have shown how the CSM model is in accord with the anatomical structure of the cones and how its dynamical aspect explains the existence of subjective colors.  Both of these aspects are notable failures of the standard, three-cone model of color vision.

There exists a vast body of scientific research and published literature on human color vision.  In part, this is a reflection of the natural interest in the functioning of one of our most profound and treasured human senses.  It is also a reflection of the confounding complexity of the perception (involving psychology, physics, neurophysiology, biochemistry, and psychophysics) and the lack of a widely accepted and truly comprehensive model to explain the myriad aspects of the phenomenology of color vision.  Given the vast array of phenomenology involved, we will not be able to address all of it here at the present time (although a lot more is covered in the book, Cone Shape and Color Vision: The Unification of Structure and Perception.)

Consider for a start what any such model of human color vision must encompass and explain.  We present here a laundry list of such properties and characteristics, a list that is extensive but by no means totally comprehensive. 

The list is divided into three categories:

I.         Anatomical and Structural Features

  1. Cone shape: The photosensitive outer segment of the photoreceptors of color vision is uniformly conical in shape as contrasted with the outer segment of the rod photoreceptors of achromatic night vision which is uniformly cylindrical.
  2. Local uniformity of cones: All the cones within a given region of the retina are histologically similar (or identical) with no physically identifiable cone classes (with the possible exception of so-called blue cones).
  3. Systematic variation of cone size and shape across retina:  The longest and most gently tapering cones are in the central retina (fovea) where color vision is best and they gradually decrease in length and become more obviously tapered as one progresses further out in the retina in accord with the decrease in color vision function in the peripheral retina.
  4. Equivalence of bipolar/cone ratio to dimensionality of color vision: There are three bipolar cells (outputs) per cone in the central retina where vision is three dimensional, decreasing to 2:1 where color vision becomes dichromatic, and 1:1 in the peripheral retina as color vision function becomes monochromatic (Missotten, 1974; Sheppard, 1968; Vilter, 1949).
  5. Small diameter of the photosensitive portion of the cones: The cone’s photosensitive outer segment is much smaller than required for spatial resolution alone and is substantially smaller than the inner segment diameter. The outer segment dimensions do appear to be ideal for low-order waveguide mode cutoff.
  6. Correlation between cone length and the color resolution provided: This is part of the systematic variation described in (I.3) above.
  7. Localization of photoabsorption events along the cone length: Absorption of light triggers a cascade of biochemical events that results in the closure of ion channels within a region one micrometer or smaller in extent along the length of the cone so that it is a local event (Holcman & Korenbrot, 2004).
  8. Numerous photopigments:  Molecular genetics have revealed the existence of a host of variants of the “red” and “green” photopigments.  These photopigments have values of their absorption peak deviating by 5 nm or so from that of the “standard” versions.
  9. Multiple photopigments within single cones: Evidence indicates that cones may have more than one photopigment within individual cones (pigment co-expression, c.f., Glösmann & Ahnelt, 2002; Jacobs, Williams, & Fenwick, 2004; Marks, Dobelle, & MacNichol, 1964; Parry and Bowmaker, 2002; Röhlich, Veen &. Szél, 1994; and Xiao & Hendrickson, 2000). For example , Jacobs, Williams, & Fenwick (2004) in demonstrating the existence of color vision in the mouse despite extensive and complete co-expression of both of the rodent's visual pigments in all cones had to conclude: “Since mice can make dichromatic color discriminations, their visual systems must be able to exploit differences in the spectral absorption properties among the cones. Complete selective segregation of opsins into individual photoreceptors is apparently not a prerequisite for color vision.” (Emphasis added.)
  10. Uniform color vision function despite wide variation in apparent “red” and “green” cone reflectances:  In MSP measurements on living retina, researchers have found enormous variation in the relative number of apparent “red” and “green” cones among different subjects (40:1 variation among subjects) with no apparent difference the subject’s color vision function (Carroll, Neitz & Neitz, 2002; McMahon, Neitz, & Neitz, 2004; Hofer, Carroll, Neitz, Neitz, & Williams, 2005).  Recall that while there are good arguments suggesting that these retinal densitometry measurements don’t necessarily indicate a unique pigment in each cone, none-the-less, the remarkable constancy of color vision function seems to be independent of variations in measured apparent photopigments.
  11. Color vision function is independent of the blotchiness of red/green cone distribution: Observations by Roorda and Williams (1999) has shown not only large inter-individual variations in the ratios of apparent cone types, but also that the mosaic of these cones is not at all regular, being essentially random and very "clumpy". None-the-less, this patchiness seems to have no effect on the individual's color vision function.
  12. Peripheral cones have scotopic spectral sensitivity: While the overall spectral sensitivity of the cones in the central retina peaks at about 555 nm in the green (photopic spectral sensitivity) in the periphery, cones have a spectral sensitivity peak at about 500 nm and their spectral sensitivity is essentially indistinguishable from the scotopic spectral sensitivity of rods (Abramov and Gordon, 1977; Weale, 1953; Wooten and Wald 1973). Thus, compared to more central cones, the peripheral cones have a more conical shape, simpler neural connectivity, poorer color discrimination function, and the spectral sensitivity of rods.

II.         Color Vision Functions

  1. Color discrimination characteristics:  Data on the characteristic curve of hue discrimination show broad minima at around 580 nm and 500 nm and a more abrupt local minimum around 440 nm while going to unbound maxima (worse discrimination) at either end of the spectrum.
  2. Spectral purity characteristics: The plot of spectral purity (difference from white, a measure of saturation) has one broad minimum around 580 nm. That is, yellow is the least saturated color and is the color that is least different from white (lowest “purity”).
  3. Unique yellow: Virtually all human observers identify a reproducibly stable monochromatic wavelength around 580 nm or so as being a pure yellow, balancing between the red and green sensations
  4. Color constancy: Human color vision has the remarkable property of the stability of perceived hue in a scene regardless of variation in the colorcast of the general illuminant used (and consequent wide variation in actual spectral content of light entering the eye). That is, the eye has a powerful ability to discount the overall color tint of the general illumination.
  5. Ordered chromatic latency of color perception: Experimental data shows that the delay in perception of monochromatic light varies systematically and monotonically with wavelength (Medeiros, 2006).  In particular red light is perceived fastest and as the wavelength is decreased, the perception is delayed linearly so that blue light is perceived about 30 msec later than red light.
  6. Similarity of violet and purple: The color violet (wavelengths shorter than about 460 nm) looks very similar to a mixture of blue and red, the color purple.  Indeed, if one looks at the output of a monochrometer as one tunes to progressively shorter wavelengths, around 460 nm it looks exactly like a component of red light is being added (rather abruptly) to the blue. Attempts to explain this perceptual similarity have postulated the existence of a subsidiary maximum at short wavelengths in the absorption spectrum of the "red" pigment. However, there is no compelling evidence for such a sub-maximum and in any case, even if it were present, it could not have the abrupt rise required to provide the similarly abrupt turn-on of the red part of the violet perception.
  7. Invariance of color perception with reversed direction of incidence: In a famous experiment Brindley and Rushton (1959) found that the perceived color of light is the same whether that light is incident on the cones in its usual (forward direction) or reversed (having passed into the retina from the back of the eye).  This result clearly rules out color vision being based on any sort of filter in front of the cones and was also originally interpreted as ruling out models based on any waveguide effects.  However, the fundamental Reversibility Theorem of optics states that the path of light through any optical system is physically the same on reversal and thus the Brindley and Rushton observation does not rule out any color selection process based on the physical transmission of light, i.e., waveguide effects.
  8. Color defective vision: There are a number of ways in which color vision fails, but by far the most common forms of “color blindness” are the two forms (protan and deutan) of red-green defective vision.  In addition to the similar (but not identical) red-green confusions for these two forms of dichromatic vision, there is a marked reduction in the sensitivity to red light in protanopes but no similar reduced sensitivity to green in deuteranopes. It has been directly demonstrated that despite the absence of the genetic machinery for one of the "red" or "green" photopigments, such dichromats can still distinguish red and green in color-naming experiments. Particularly telling in this regard are the results of Watcher, Dohrmann, and Hertel (2004). Quoting from their paper: "Protanopes and deuteranopes, despite lacking a chromatic dimension at the receptor level, use the color terms ‘‘red’’ and ‘‘green’’, together with ‘‘blue’’ and ‘‘yellow’’, to describe their color percepts. Color vision models proposed so far fail to account for these findings in dichromats. We confirmed, by the method of hue scaling, the consistent use of these color terms, as well as their dependence on intensity, in subjects shown to have only a single X-chromosomal opsin gene each."
  9. Color anomalous vision: In addition to the extreme forms of red-green color blindness, there also exist anomalous forms of defective color vision (protanomalous and deuteranomalous) spanning a gradation in function from the extreme forms with (near) total inability to discriminate reds and greens to virtually normal color vision.  Protanomalous (“red-blind”) subjects, for example, were found with “red” and “green” pigments that had identical peak sensitivities, but yet had (limited) red-green color discrimination (Neitz, Neitz, He, and Shevell 1999).
  10. Individual cones elicit any color sensation, including white: In a recent, very fascinating, experiment (Hofer, Singer, and Williams, 2005) used an adaptive optics technique to illuminate single cones in the living eye.  They found that, regardless of the color of illuminant they used, the color perceived by any one cone could be any color, including the sensation of white.
  11. Photochromatic Interval:  Better termed the achromatic interval where, as the brightness of a monochromatic light is decreased it changes from being colored to being gray (or white) near threshold for all wavelengths except red.  This interval is largest for the shortest wavelengths and smallest for the longer wavelengths.
  12. Blue component of violet perceived before red component at threshold: At low intensities of short-wavelength light, as the intensity is brought up from subthreshold values, the blue sensation is perceived first and the ‘added’ red component of violet is seen only later at higher intensities (Gothlin, 1944).
  13. Electrophysiological response of the eye to alternating colored lights: Shown to be directly proportional to the difference in wavelength of the lights (Riggs, Johnson, and Schick 1966).
  14. Pupil dilation response of the eye to alternating colored lights: Shown to be directly proportional to the difference in wavelength of the lights (Young and Alpern, 1980).

III.         Color Vision Effects

  1. Breakdown of statically established metameric matches under dynamic conditions: Ives (1918) demonstrated in his paper, “Resolution of mixed colors” that a mixture of red and green that looked yellow, resolved into a red leading edge and a green trailing edge as a bar of the mixed light was moved across the retina while a pure monochromatic yellow that matched the mixture under static presentation, did not similarly resolve when moved.  My colleagues and I have repeated this experiment with the same result.  This experimental result flatly contradicts the standard three cone model of color vision.
  2. Subjective colors (Fechner-Benham colors):  This is the invocation of ordered color perception with intermittent achromatic illumination and the correlation of the order of the induced colors with a systematic temporal code with time constants the same as measured for differential chromatic latency.  While the perceived subjective colors are somewhat desaturated, they are universally seen in the same spectral ordering by all observers with normal color vision.
  3. Loss of color vision under image stabilization: It is found that there is a rapid and complete loss of vision, particularly color vision, when the image on the retina is static (stabilized).
  4. Fluttering Heart Effect: This is a perceived lagging of a colored target on a background of a different color when the two are oscillated together. For example, the effect is easily invoked with a blue target on a red background where the blue target is seen to "lag" behind the red background. Helmholtz (1867) was the first to clearly suggest that the effect is caused by a difference in the perceptual latencies of different colors. Clearly this is in accord with the measurements we have discussed on the differential chromatic latency, an effect necessary for the proposed CSM model but rather mysterious in the context of the three-cone model.
  5. Stiles-Crawford color change: Also known as the Stiles Crawford effect of the Second Kind or SC-II, where the perceived color of a monochromatic light changes as the angle of incidence of the light at the retina is changed (Stiles, 1937; Alpern, 1986).  The better-known SC-I effect is the reduction in intensity of a light as its angle of incidence at the retina is increased.  The SC-II effect is predominantly a red shift with increasing angle of incidence, uniformly so for small angles, and mostly so for all angles and colors.  Explanations of this effect within the context of the trichromatic model have been proposed previously in terms of pigment self-screening effects (e.g., Walraven & Bouman, 1960). Experimental measurements contradict such explanations. For example, Wooten, et al (1978) examined the effect for conditions where much of the visual pigment had been bleached but the effect was still present, ruling out self-screening explanations. In the end, they stated "... we must conclude that the only framework that is capable of accounting for our high bleach measurements is waveguide theory." In fact, the shift is well modeled by a wavelength change proportional to [1/cos(ø)] where ø is the angle of incidence (Medeiros, 1979, 2006). We compare this function, a direct consequence of the CSM model, with the experimental data on the SC II effect in the book, Cone Shape & Color Vision where an excellent fit is demonstrated.
  6. Bezold-Brüke Effect: This is the change in perceived color of a monochromatic light as its intensity is varied.  While the exact details are somewhat complex, the primary effect as intensity is increased is a shift to shorter wavelengths for light with a wavelength longer than 580 nm (red light shifts toward yellow) and a shift to longer wavelengths for light with a wavelength shorter than about 580 nm.
  7. Abney Effect: This effect involves a change in the apparent hue of a monochromatic light with the addition of white light (Abney, 1909; Kurtenbach, et al, 1984). For example, addition of white light to red changes the apparent hue towards yellow.
  8. Tyndall’s Paradox: The paradoxical improvement in hue discrimination with the addition of white light to a monochromatic light (especially in the blue region of the spectrum).  First noted by Tyndall (1933) and subsequently explored in more depth by Mollon and Estevez (1988).
  9. Constancy of white perception across the retina: While colored lights are perceived differently in different parts of the retina, white is perceived the same even though the eye has a remarkable sensitivity to differences in the appearance of a white illuminant (Hartridge, 1948).
  10. Blue Arcs of the Retina: When an area near the fovea is stimulated by (virtually) any color of light, blue colored arcs (or spikes if the illumination is between the fovea and optic disc) are seen following the pathway of the ganglion cells sending signals from the illuminated area to the optic disc.  The phenomenon is clearly due to induced signals from parallel fibers (Alpern and Dudley, 1966), but why is the induced color blue (c.f., Ingling & Drum, 1977)?
  11. Land Effect: As demonstrated by Edwin Land in the 1950’s and 1960’s, it is found that only a wavelength difference in two superimposed projections is needed to reproduce the full range (albeit desaturated) of perceived colors (Land, 1959). For example, if two recordings of a natural scene are made, one through a filter with a long wavelength passband and one through a filter with a short wavelength passband, then if the recorded long-wavelength scene picture is projected through a red filter and the short-wavelength record is projected with no filter (black and white only) and the two projections are superimposed, then the projected scene will have natural and correct coloration exhibiting virtually the full range of spectral colors. This is an astonishing departure from what might superficially be expected from such a two-color projection, namely a scene with a general pink (desaturated red) cast with no properly ordered colors. Evidently the human color vision system can interpolate the full range of correct colors from just the ordered projection of the record of the long-wavelength and short-wavelength portions of a scene.
  12. Chromatic adaptation: when a colored background illuminant is used, the spectral sensitivity of the eye changes in very particular ways (c.f. Boynton, et al 1959; Boynton, 1956; MacAdam, 1956; Speelman and Krauskopf, 1963; Delahunt and Brainard, 2000) . To a rough approximation, red sensitivity is most strongly affected (reduced) by adaptation to any background color.
  13. Violation of univariance : Brown (1983) reported measurements of the time course of dark adaptation after exposure to different colors (supposedly equated for "red" or long wavelength sensitive cones) that showed clear violations of the so-called Principle of Univariance (Naka and Rushton, 1966). That principle was formulated as the underpinning of the three-cone model to state that the output of a receptor was to be only dependent on its total quantal catch of light and to be independent of wavelength. Similar violations of the "Principle of Univariance" were also noted by Augenstein and Pugh (1977), Pugh and Mollon (1979), Fuortes, Schwartz, and Simon (1973), and others. Note that in the CSM model we have proposed here, that the output of the cones is not fundamentally different for different wavelengths. Different colors of inputs to the cones simply give different rise (and fall) times of their output signal as the input is modulated.
  14. Breakdown of color matches with high intensities of adaptation: Wright (1936) observed that for a yellow initially matched by a red and green mixture, after adaptation to very bright light, the match was no longer satisfactory, generally requiring more red in the mixture for a match (further explored and verified by Brindley, 1953). Such an effect violates the standard laws of additivity (Grassman's Laws) as it is generally understood to be required by the three-cone model.
  15. Special significance of yellow: Observers can readily and consistently identify a unique yellow (with either no reddish or greenish tint) and this unique yellow remains invariant for each observer across a wide range of observing and viewing conditions (Abramov and Gordon, 2005). Moreover, the wavelength of this unique yellow (usually in the range of 575-585 nm) corresponds to the position of both the least saturated color and the location of best color discrimination.
  16. Special properties of blue light: The color blue has long been known to exhibit some unique features, including a very high chromaticity value (Mollon, 1977). That is, blue light contributes to chromatic value of a patch of light more strongly than any other color. Moreover, under conditions of rigid fixation, blue perception is preferentially lost before other chromatic perceptions in an effect known as small-field tritanopia (McCree, 1960, Wright, 1977). In the CSM model, blue light is uniquely present in the most distal portion of the cones so that the last-to-arrive signal from a cone uniquely signals the presence of a blue component of incident light.

This is quite a list (42 items in three categories). I would not even suggest that the list is exhaustive.  The fact is that the standard, widely accepted, three-cone model of human color vision explains almost none of the items on this list in a straightforward and non-contrived fashion.  Indeed that model is flatly contradicted by much of what is on the list.  Given this state of affairs, it is somewhat incredible that the standard model is so widely and dogmatically held and that so little credence has been given to efforts to find some better way to explain color vision. To make the inadequacy of the standard three-cone model of color vision more apparent, I have included a chart of these 42 properties and effects and the way the proposed CSM model compares with the standard model in terms of explaining these characteristics. While the exact assignment of how well each model might or might not explain or be consistent with each of the listed properties may be somewhat up for interpretation, depending on your point of view, I have tried to be conservative in my assignment of success (green), indifference (yellow), or failure (red) of each model. Even, allowing that I might have a somewhat biased view of these issues, the dichotomy between the two approaches to explaining human color perception is still rather stark.

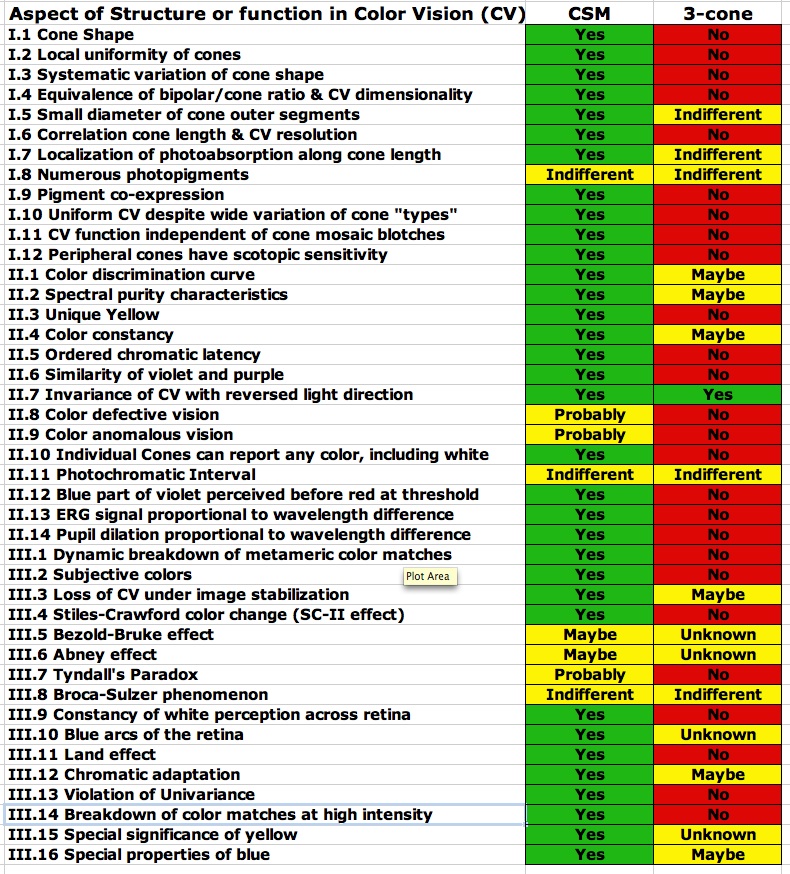
Many of the 42 items on the list are directly addressed in the current document (including further discussion below) and most of the rest are covered in the book, Cone Shape & Color Vision. A few of the items on the list are not directly addressed either here or in the book (about four or five such items). I do plan to cover these, as well as other items not mentioned in this list, in future publications.

Despite the evident failures of the trichromatic theory, part of the resistance to abandoning the model is that color vision clearly is (at least to a first approximation) three-dimensional (as in three primaries required for metameric matches) and that three cone classes are an easy way to explain this.  However, the widely ignored evidence is that, as noted above (I. 4.) the dimensionality of color vision is more closely associated with the number of bipolar outputs per cone.  Moreover, the Ives (1918) experimental result flatly contradicts the three-cone model and proves it cannot be right.  None-the-less this and other evidence from the list above has long been ignored as many in the field have insisted on fitting the phenomenology to the three-cone model.

In contrast, the cone spectrometer model (CSM) I have proposed has none of these contradictions; it is consistent with all of the experimental evidence, and goes a long way towards explaining every one of the features mentioned in the above three-part list of structure, function, and phenomenology.  The CSM theory directly makes use of the small size and conical taper of the retinal cones to sort the visible spectrum along the length of the cone through low-order waveguide mode cutoff.  The ordered spectral information along the cone length is then read out in a time-ordered code that uses microsaccadic eye movements for a temporal reference.   The resulting time-ordered color information then directly explains the Ives (1918) result, our measurements of chromatic latency, and the details of subjective (Fechner-Benham) colors.

Virtually all the items on the above list are addressed in terms of CSM in the book,

Cone Shape & Color Vision: The Unification of Structure and Perception. 

The book is available as a soft cover volume (figures in black and white only) or as a downloadable PDF file (with figures in color) from all the standard on-line booksellers such as Amazon.com, Barnes & Noble, etc.

Some of the items addressed in greater detail in the book include:

The book also has more in-depth coverage of the experiments on the separation of rod and cone perception.  A good idea of what is covered in the book can be gleaned from the table of contents found here. 

 

Next: Hue Discrimination and the Similarity of Violet and Purple

Back to the Beginning